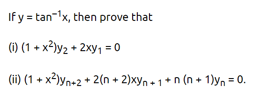Higher Order Derivatives
IMPORTANT
Higher Order Derivatives: Overview
This Topic covers sub-topics such as Finding Higher Order Derivatives and Higher Order Derivatives & Partial Derivatives
Important Questions on Higher Order Derivatives
HARD
IMPORTANT
The function satisfies for all real Given that and compute the value of
HARD
IMPORTANT
If then then find the value of
HARD
IMPORTANT
If Then what would be the value of
EASY
IMPORTANT
If , then what would be the value of given expression
MEDIUM
IMPORTANT
Find the directional derivative of at in the direction of vector